2024年8月21日,深圳大學高等研究院閆昇團隊將其成果以“Deciphering the Evolution of Inertial Migration in Serpentine Channels”為題的論文,發表于Analytical Chemistry。深圳大學高等研究院和機電與控制工程學院聯合培養碩士生劉勇為論文第一作者,深圳大學高等研究院研究員閆昇、深圳大學機電與控制工程學院副教授彭小波為通訊作者。該工作還得到澳大利亞格里菲斯大學博士張俊的支持。

圖1.本報道被選為Analytical Chemistry的期刊封面
蛇形流道耦合慣性流和二次流,可實現有效的顆粒聚焦和分離,在臨床診斷和藥物篩選中顯示出巨大的潛力。然而,蛇形流道中的不穩定的二次流使得慣性遷移的演化不明確,阻礙了蛇形流道的發展和應用。為了完善慣性遷移機理,本研究建立了一個具有不同曲率比的模型,研究了二次流對蛇形流道中顆粒遷移的影響。該方法采用直接數值模擬計算慣性升力,將慣性升力映射到蛇形流道的橫截面,并利用拉格朗日粒子跟蹤方法破譯慣性遷移。通過實驗研究了顆粒的慣性遷移,驗證了所建立的數值模型。結果表明,蛇形流道中的顆粒遷移遵循二階遷移理論。增加二次流會加速第二階段的遷移,并減慢第一階段的遷移。此外,本文研究了雷諾數、截面高寬比和阻塞率等不同參數對粒子平衡位置的影響,為粒子的高分辨率分離提供了指導。在考慮到流動阻力的前提下,本文的無量綱研究使得任意大小的顆粒的分離成為可能。本研究揭示了蛇形流道中的遷移機制,為顆粒的慣性分離提供了新的契機。
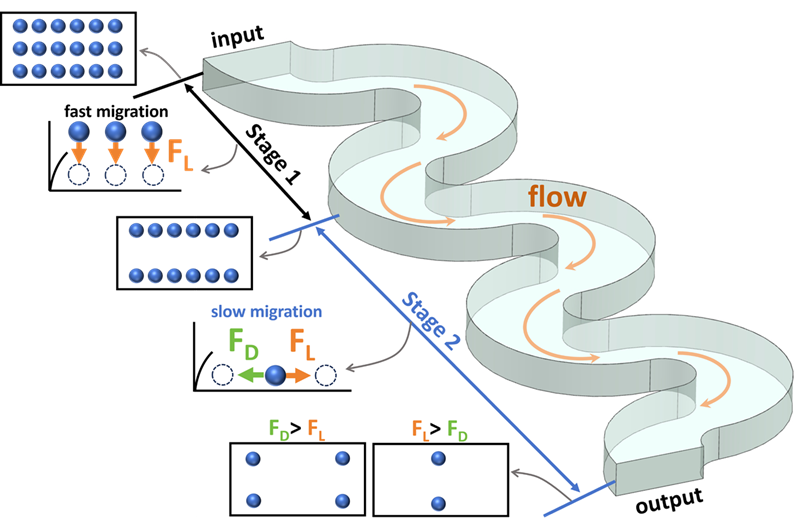
圖2.蛇形流道中顆粒的二階遷移
該成果得到國家自然科學基金、珠江人才計劃、廣東省基礎與應用基礎研究基金和深圳大學卓越研究計劃的支持。
原文鏈接:https://pubs.acs.org/doi/10.1021/acs.analchem.4c03474





